
신장 트리란?
신장 트리(spanning tree)란 그래프 내의 모든 정점을 포함하는 트리이다.
신장 트리도 트리의 일종이므로 모든 정점들이 연결되어 있고, 사이클이 없어야 한다.
신장 트리는 그래프의 n개의 정점을 (n - 1)개의 간선으로 연결한다.
신장 트리를 찾기 위해 DFS, BFS를 이용할 수 있고, 하나의 그래프에는 많은 신장 트리가 존재한다.

최소 비용 신장 트리란?
최소 비용 신장 트리(MST, minimum spanning tree)는 가중치 그래프의 모든 정점들을 가장 적은 수의 간선과 비용으로 연결한 트리이다.
즉, 어떤 그래프의 신장 트리들 중에서 사용된 간선들의 가중치 합이 가장 작은 신장 트리이다.
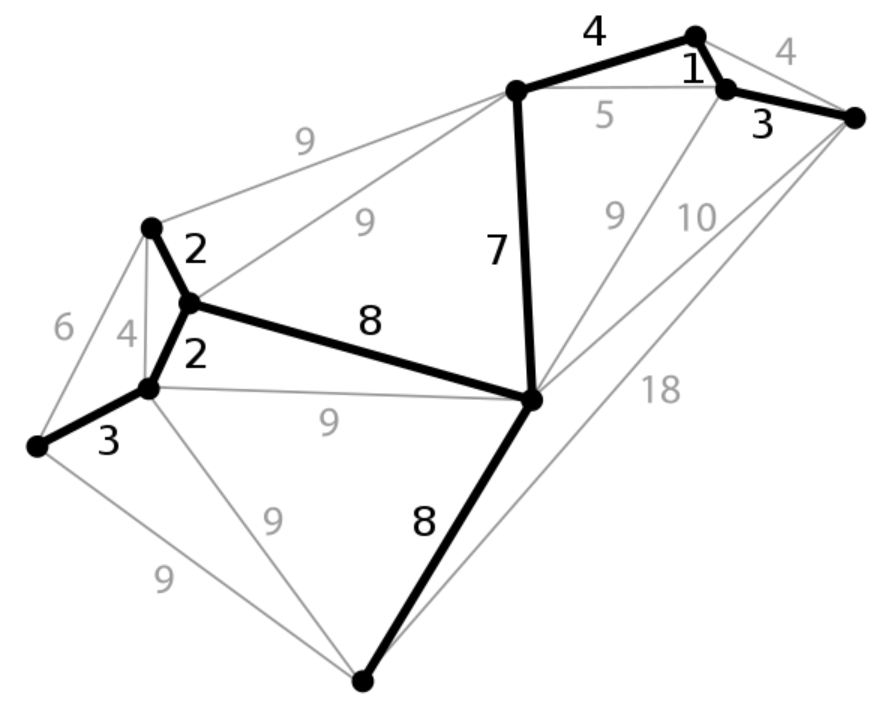
MST는 실생활의 다양한 곳에서 활용된다.
- 도로 건선 : 도시들을 모두 연결하면서 도로 설치 비용이 최소가 되도록 하는 문제
- 전기 회로 : 단자들을 모두 연결하면서 전선의 길이가 최소가 되도록 하는 문제
- 배관 : 원하는 모든 장소를 연결하면서 사용된 전체 파이프의 길이를 최소가 되도록 하는 문제
MST는 다음 조건을 반드시 만족해야 한다.
(1) 간선의 가중치 총합이 최소여야 한다.
(2) 반드시 (n - 1)개의 간선만 사용해야 한다.
(3) 사이클이 포함되어서는 안된다.
MST를 구하는 방법으로는 대표적으로 Kruskal 알고리즘과 Prim 알고리즘이 있다.
'Computer Science > Data Structure' 카테고리의 다른 글
| 10-5. [C/C++] MST를 위한 Prim 알고리즘 (0) | 2023.08.16 |
|---|---|
| 10-4. [C/C++] MST를 위한 Kruskal 알고리즘 (0) | 2023.08.16 |
| 10-2. [C/C++] 인접 행렬을 이용한 가중치 그래프의 구현 (0) | 2023.08.16 |
| 10-1. 가중치 그래프란? (0) | 2023.08.16 |
| 9-5. [C/C++] 그래프의 탐색 - 너비 우선 탐색, BFS (0) | 2023.08.09 |
